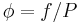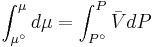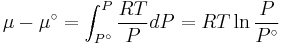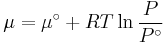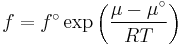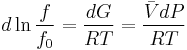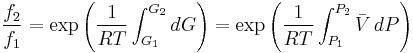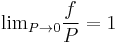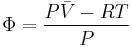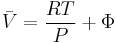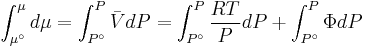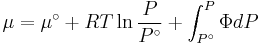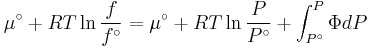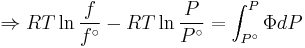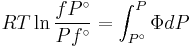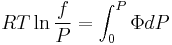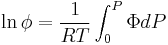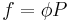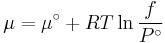Fugacity
In chemical thermodynamics, the fugacity ( ) of a real gas is an effective pressure which replaces the true mechanical pressure in accurate chemical equilibrium calculations. It is equal to the pressure of an ideal gas which has the same chemical potential as the real gas. For example, nitrogen gas (N2) at 0°C and a pressure of 100 atm has a fugacity of 97.03 atm.[1] This means that the chemical potential of real nitrogen at a pressure of 100 atm has the value which ideal nitrogen would have at a pressure of 97.03 atm.
) of a real gas is an effective pressure which replaces the true mechanical pressure in accurate chemical equilibrium calculations. It is equal to the pressure of an ideal gas which has the same chemical potential as the real gas. For example, nitrogen gas (N2) at 0°C and a pressure of 100 atm has a fugacity of 97.03 atm.[1] This means that the chemical potential of real nitrogen at a pressure of 100 atm has the value which ideal nitrogen would have at a pressure of 97.03 atm.
Fugacities are determined experimentally or estimated for various models such as a Van der Waals gas that are closer to reality than an ideal gas. The ideal gas pressure and fugacity are related through the dimensionless fugacity coefficient 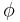 .[2]
.[2]
For nitrogen at 100 atm, the fugacity coefficient is 97.03 atm / 100 atm = 0.9703. For an ideal gas, fugacity and pressure are equal so 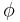 is 1.
is 1.
The fugacity is closely related to the thermodynamic activity. For a gas, the activity is simply the fugacity divided by a reference pressure to give a dimensionless quantity. This reference pressure is called the standard state and normally chosen as 1 atmosphere or 1 bar, Again using nitrogen at 100 atm as an example, since the fugacity is 97.03 atm, the activity is just 97.03 without units.
Accurate calculations of chemical equilibrium for real gases should use the fugacity rather than the pressure. The thermodynamic condition for chemical equilibrium is that the total chemical potential of reactants is equal to that of products. If the chemical potential of each gas is expressed as a function of fugacity, the equilibrium condition may be transformed into the familiar reaction quotient form (or law of mass action) except that the pressures are replaced by fugacities.
For a condensed phase (liquid or solid), the chemical potential is equal to that of the vapor in equilibrium with the condensed phase, and therefore the fugacity is equal to the fugacity of the vapor. This fugacity is approximately equal to the vapor pressure when the vapor pressure is not too high.
The word "fugacity" is derived from the Latin for "fleetness", which is often interpreted as “the tendency to flee or escape”. The concept of fugacity was introduced by American chemist Gilbert N. Lewis.[3]
Contents |
Definition in terms of chemical potential
The fugacity of a real gas is formally defined by an equation analogous to the relation between the chemical potential and the pressure of an ideal gas.
For any pure substance, the chemical potential (μ) is equal to the molar Gibbs free energy, whose variation with temperature (T) and pressure (p) is given by 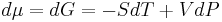 . At constant temperature, this expression can be integrated as a function of
. At constant temperature, this expression can be integrated as a function of  . We must also set a reference state. For an ideal gas the reference state depends only on pressure, and we set
. We must also set a reference state. For an ideal gas the reference state depends only on pressure, and we set  = 1 bar so that
= 1 bar so that
Now, for an ideal gas 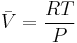
Reordering, we get
This gives the chemical potential for an ideal gas in an isothermal process, with a reference state is  = 1 bar.
= 1 bar.
For a real gas, we cannot calculate 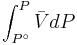 because we do not have a simple expression for a real gas’ molar volume. Even if using an approximate expression such as the van der Waals equation, the Redlich-Kwong or any other equation of state, it would depend on the substance being studied and would be therefore of very limited utility.
because we do not have a simple expression for a real gas’ molar volume. Even if using an approximate expression such as the van der Waals equation, the Redlich-Kwong or any other equation of state, it would depend on the substance being studied and would be therefore of very limited utility.
We would like the expression for a real gas’ chemical potential to be similar to the one for an ideal gas. We therefore define a magnitude, called fugacity, so that the chemical potential for a real gas becomes
with a given reference state to be discussed later. This is the usual form of the definition, but it may be solved for f to obtain the equivalent explicit form
Evaluation of fugacity for a real gas
Fugacity is used to better approximate the chemical potential of real gases than estimations made using the ideal gas law. Yet fugacity allows the use of many of the relationships developed for an idealized system.
In the real world, gases approach ideal gas behavior at low pressures and high temperatures; under such conditions the value of fugacity approaches the value of pressure. Yet no substance is truly ideal. At moderate pressures real gases have attractive interactions and at high pressures intermolecular repulsions become important. Both interactions result in a deviation from "ideal" behavior for which interactions between gas atoms or molecules are ignored.
For a given temperature 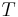 , the fugacity
, the fugacity 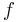 satisfies the following differential relation:
satisfies the following differential relation:
where  is the Gibbs free energy,
is the Gibbs free energy, 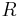 is the gas constant,
is the gas constant, 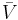 is the fluid's molar volume, and
is the fluid's molar volume, and 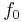 is a reference fugacity which is generally taken as 1 bar. For an ideal gas, when
is a reference fugacity which is generally taken as 1 bar. For an ideal gas, when 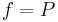 , this equation reduces to the ideal gas law.
, this equation reduces to the ideal gas law.
Thus, for any two physical states at the same temperature, represented by subscripts 1 and 2, the ratio of the two fugacities is as follows:
For an ideal gas, this becomes simply 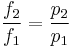 or
or 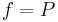
But for 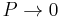 , every gas is an ideal gas. Therefore, fugacity must obey the limit equation
, every gas is an ideal gas. Therefore, fugacity must obey the limit equation
We determine  by defining a function
by defining a function
We can obtain values for 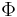 experimentally easily by measuring
experimentally easily by measuring  ,
,  and
and  .
.
From the expression above we have
We can then write
Where
Since the expression for an ideal gas was chosen to be 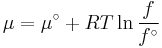 ,we must have
,we must have
Suppose we choose  . Since
. Since 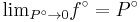 , we obtain
, we obtain
The fugacity coefficient is defined as  = f/P (note that for an ideal gas,
= f/P (note that for an ideal gas,  = 1.0), and it will then verify
= 1.0), and it will then verify
The integral can be evaluated via graphical integration if we experimentally measure values for 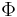 while varying
while varying  .
.
We can then find the fugacity coefficient of a gas at a given pressure  and calculate
and calculate
The reference state for the expression of a real gas’ chemical potential is taken to be “ideal gas, at  = 1 bar and temperature
= 1 bar and temperature  ”. Since in the reference state the gas is considered to be ideal (it is an hypothetical reference state), we can write that for the real gas
”. Since in the reference state the gas is considered to be ideal (it is an hypothetical reference state), we can write that for the real gas
See also
- Activity (chemistry), the measure of the “effective concentration” of a species in a mixture
- Chemical equilibrium
- Electrochemical potential
- Excess chemical potential
- Partial molar property
- Thermodynamic equilibrium
- Fugacity capacity
References
- ^ Peter Atkins and Julio de Paula, Atkins' Physical Chemistry (8th edn, W.H. Freeman 2006), p.112
- ^ Atkins, Peter; John W. Locke (2002-01). Atkins' Physical Chemistry (7th ed.). Oxford University Press. ISBN 0198792859.
- ^ Lewis, Gilbert Newton (1908-05-01). "The Osmotic Pressure of Concentrated Solutions, and the Laws of Perfect Solution.". Journal of the American Chemical Society 30 (5): 668–683. doi:10.1021/ja01947a002.